What is Power Triangle ? or active power, reactive power and apparent power

What is power triangle ? Active power, Reactive power and Apparent power ?

The analysis of power factor can also be made in terms of power drawn by the a.c. circuit. If each side of the current triangle OAB is multiplied by voltage V , then we get the power triangle OAB shown in fig below

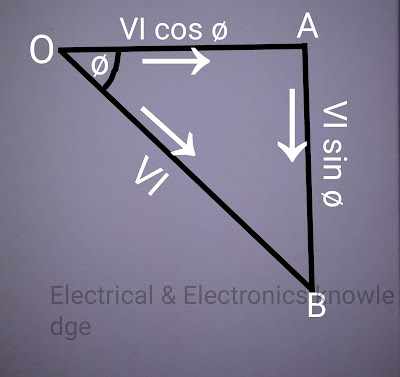Power Triangle

OA = VI cos ø and represents the active power in watts or kW

AB = VI sin ø and represents the reactive power in VAR or kVAR

OB = VI and represents the apparent power in VA or kVA

The following points my be noted from the power triangle :

• The apparent power in an a.c. circuit has two components active and reactive power at right angles to each other.

         OB² = OA² + AB²         

or, (apparent power)² = (active power)² + (reactive power)²

or (kVA)² (kW)² + (kVAR)²

• Power factor, cos ø = OA\ OB 

   Or, active power\apprent power = kV \ kVA

Thus the power factor of a circuit may also be defined as the ratio of active power to the apparent power. This is perfectly general definition and can be applied to all cases, whatever be the waveform.

• The lagging reactive power ( If the current lags behind the voltage, the reactive power drawn is known as lagging reactive power. However, if the circuit current leads the voltage, the reactive power is known as leading reactive power.) Is responsible for the low power factor. It is clear from the power triangle that smaller the reactive power component, the higher is the power factor of the circuit.

     kVAR = kVA sin ø kW\cos ø × sin ø

     kVAR = kW tan ø

• For leading current, the power triangle becomes reversed. This fact provides a key to the power factor improvement. If a device taking leading reactive power (e.g. capacitor) is connected in parallel with the load, then the lagging reactive power of the load will be partly neutralised, thus improving the power factor of the load.
• The power factor of a circuit can be defined in one of the following three ways :

1. Power factor = Cos ø = cosine of angle between voltage (V) and current (C)
2. Power factor = R\Z = Resistance\Impedance
3. Power factor = VI cos ø\VI = Active power\Apparent power.

• The reactive power is neither consumed in the circuit nor it does any useful work. It merely flows back and forth in both directions in the circuit. A wattmeter does not measure reactive power.

Example: Let us illustration of power relations in an a.c. circuit with an example. 

Suppose a circuit drawn a current of 10 A at a voltage of 200 V and it's p.f. is 0.8 lagging. Then

 Apparent power = VI = 200 × 10 = 2000VA

 Active power = VI cos ø = 200 × 10 × 0.8 = 1600 W

 Reactive power = VI sin ø = 200 × 10 × 0.6 = 1200 VAR

The circuit reactive an apparent power of 2000 VA and is able to convert only 1600 Watt into active power. The reactive power is 1200 VAR and does not useful work. It merely flows into and out of the circuit periodically. In fact, reactive power is a liability on the source because the source has to supply the additional current (i.e., I sin ø).

• Tweet
• Share
• Share
• Share
• Share

About Admin MC3

This is dummy text. It is not meant to be read. Accordingly, it is difficult to figure out when to end it. But then, this is dummy text. It is not meant to be read. Period.

Related Post