Voltage control by Synchronous condenser:
The voltage at the receiving end of a transmission line can be controlled by installing specially designed synchronous motors called synchronous condenser at the receiving end of the line. The synchronous condenser supplies wattless leading kVA to the line depending upon the excitation of the motor.
 |
| Synchronous condensed |
This wattless leading kVA party or fully cancels the wattless lagging kVA of the line, thus controlling the voltage drop in the line. In this way, voltage at the receiving end of a transmission line can be kept constant as the load on the system changes.
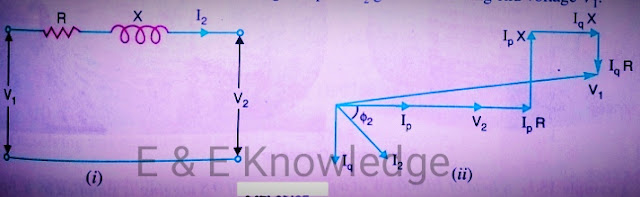
For simplicity, consider s short transmission line where the effects of capacitance are neglected. Therefore, the line has only resistance and inductance. Let V1 and V2 be the per phase sending end and receiving end voltages respectively. Let I2 be the load current at a lagging power factor of cos ø2.
1. Without synchronous condenser:
(i) shows the transmission line with resistance R and inductive reactance X per phase. The load current I2 can be resolved into two rectangular components viz Ip in phase with V2 and Iq at right angles to V2 see the fig (i).
 |
| With and without synchronous condenser diagrams |
Each component will produce resistive and reactive drops ; the resistive drops being in phase with end the reactive drops in quadrature leading with the corresponding currents. The vector addition of there voltage drops to V2 given the sending end voltage V1.
2. With synchronous condenser :
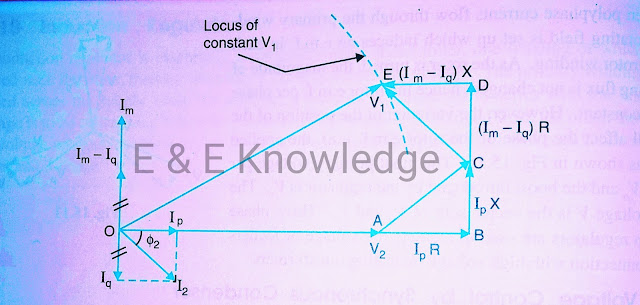
Now suppose that a synchronous condenser taking a leading current Im is connected at the receiving end of the line. Note that since I'm Iq are direct opposition and than Im must be greater than Iq, the four drop due to these two currents simplify to. The vector diagram of the circuit becomes as shown in fig below :
 |
| Vector diagram of with synchronous condenser |
(Im - Iq) R in phase with Im
And, (Im - Iq) X in quadrature leading with Im
From the vector diagram, the relation between V1 and V2 is given by;
OE² = (OA + AB - DE)² + (BC + CD)²
Or, V1² = [ V2 + IpR - (Im - Iq) X]² + [IpX + (Im -Iq) R]²
From this equation the value of Im can be calculated to obtain any desired ratio of V1/V2 for a given load current and power factor.
kVAR capacity of condenser = 3V2 Im/1000
This is dummy text. It is not meant to be read. Accordingly, it is difficult to figure out when to end it. But then, this is dummy text. It is not meant to be read. Period.
Please do not enter any spam link in the comment box. ConversionConversion EmoticonEmoticon